O problema da progressão em nível
Neste artigo pretende-se analisar a Tabela de Avanço de Nível, demonstrando como os requisitos exponenciais de Pontos de Experiência (XP) para passar de nível são incompatíveis com os ganhos lineares de XP auferidos pelos personagens. Por fim, propõe soluções para o problema.
Introdução
Sobre Tabelas de Experiência
Na maioria dos RPGs com evolução de personagens baseada em níveis, a progressão de nível por ganho de Pontos de Experiência (XP) pode ser do tipo aritmética, exponencial, logarítmica ou polinomial. E ainda pode ser mista: misturando mais de um tipo ou mais de uma função do mesmo tipo para determinadas faixas de níveis.
Na progressão aritmética a quantidade de XP necessária para passar ao nível seguinte é sempre a mesma a cada nível, formando uma linha reta em um gráfico, ou seja, progride de forma linear. Na exponencial é cada vez maior. Na logarítmica ela cresce abruptamente até certo nível e depois vai se estabilizando num crescimento suave. Na polinomial não há um padrão, depende da função adotada. Em certos trechos do gráfico polinomial a progressão pode parecer exponencial no começo e logarítmica depois, isso porque gráficos polinomiais podem fazer muitas curvas.
No clássico Dungeons & Dragons (D&D) – o RPG que inventou a evolução por níveis – cada edição adotou uma fórmula. Do antigo Rules Cyclopedia até o Advanced Dungeons & Dragons (1ª e 2ª edições), a progressão era visivelmente mista: exponencial mais ou menos até o 9º nível e linear a partir daí. Na 3ª edição a progressão era exclusivamente polinomial, adotando uma função simples e elegante: XP = 500 × (n2 - n). Toda essa simplicidade e elegância se perderam nas 4ª e 5ª edições, que adotaram polinômios de 5º grau ou maior! E nenhuma das funções que se possa encontrar parece refletir muito bem a tabela de XP adotada pelos game designers da Wizards of the Coast.
Experiência no Sistema Daemon
No sistema Daemon, a progressão em níveis existe desde a primeira edição do sistema (Arkanun, 1995; Trevas, 1997), com 10 níveis de evolução, porém não havia pontos de experiência ou coisa do tipo. Até a 2ª edição era o Mestre quem avaliava o progresso dos personagens e determinava quando passariam de nível. A evolução por ganho de XP só foi adotada na 3ª edição, que também acrescentou níveis até o 15º.
Sempre que uma aventura ou conjunto de aventuras terminar, o Mestre avalia cada personagem e decide quais estão aptos a aumentar seus níveis (geralmente a cada três ou quatro aventuras). Não há Pontos de Experiência ou coisa do tipo. Caso o Mestre decida que um Personagem aumentou de nível, ele e o jogador devem anotar todas as mudanças na Ficha de Personagem. — In: Arkanun, 1ª edição, p.50.
Sempre que uma aventura ou conjunto de aventuras terminar, o Mestre deve avaliar cada personagem e decidir quais estão aptos a aumentar seus níveis de conhecimento (geralmente a cada três ou quatro aventuras). Caso o Mestre decida que um Personagem aumentou de nível, ele deve se sentar com o jogador e anotar todas as mudanças em sua ficha de personagem.
— In: Arkanun, 2ª edição, p. 48.
A 3ª edição foi publicada em 2000, com o livro Arkanun, e em 2001 foi lançado o Trevas. Nesse mesmo período temos o tsunami causado pela Open Game License (OGL) e pelo Sistema d20, que liberou gratuitamente o sistema da 3ª edição de D&D. O impacto foi tão grande que a Daemon Editora tentou surfar nessa onda e colocou a bendita XP em sua tabela. A evolução natural do Sistema Daemon foi atropelada pelo Sistema d20...
Seja como for, à primeira vista, a função adotada desde a 3ª edição parece ser exponencial, seguindo alguma variação da equação básica de Daemon: Y = K × 2A/6, mas não é. A função que melhor representa a curva de experiência no Sistema Daemon é um polinômio de 5º grau:
n(56n4 – 883n3 + 7496n2 – 6242n + 17833) / 10.000Onde "n" é o nível, e o resultado da equação é a XP necessária para chegar naquele nível (arredondando). Não que a equação seja relevante para esta discussão, foi colocada aqui apenas para registro (foi difícil encontrar!).
O Problema
O problema está na disparidade na progressão do ganho de XP (distribuída ao fim de cada aventura) em relação à progressão de nível em si (Tabela de Avanço de Nível), isto é, a progressão de nível é polinomial, mas o ganho de XP é aritmético! Vamos voltar ao caso D&D para entender isso melhor.
Como visto, em D&D 3.ed. a progressão era polinomial, o que significa dizer que a XP necessária para passar ao nível seguinte era sempre maior do que a que foi necessária para chegar ao nível atual. Por exemplo, para passar do nível 1 ao 2 era preciso 1.000 XP, mas para passar do nível 2 ao 3 era preciso mais 2.000 (isto é, 3.000 no total), e do 3 ao 4 eram precisos outros 3.000 XP (6.000 no total), e por aí vai. Essa progressão só era possível porque os desafios também aumentavam e as recompensas em XP também: as criaturas que os personagens enfrentavam eram cada vez mais poderosas e proporcionavam cada vez mais XP. Por isso a passagem de nível dos jogadores era quase linear, o que deixa tudo interessante aos jogadores, porque eles percebem mais facilmente a sua evolução e podem se planejar. Em síntese: a progressão era polinomial, mas o ganho de XP também era! E esta lógica é válida para qualquer edição de D&D.
De volta ao Daemon. Aqui a progressão é polinomial, o que não tem problema algum. Só que o ganho de XP é aritmético! Em vez de ganhar cada vez mais XP (ganho polinomial) os jogadores ganham XP de forma fixa (linear), nunca sendo superior a 10 a cada aventura. Na média os jogadores ganham de 5 XP por aventura, o próprio Arkanun recomenda ficar entre 3 e 7 (média 5).
Pra perceber o tamanho do problema, olhem a tabela de progressão de nível do Sistema Daemon: considerando ganhos médios de 5 XP por aventura, para passar do 1º ao 2º nível são necessários apenas 5 XP, o que se consegue em apenas uma aventura. Já para evoluir do nível 6º ao 7º são necessários 40 XP (=120-80), o que se consegue em 8 aventuras. São 8 aventuras para subir um único nível. E a coisa piora em níveis mais altos: do 9º ao 10º são 150 XP em 30 aventuras; do 14º ao 15º são 600 XP em 120 aventuras. E para ir do 1º ao 15º nível são necessários 2.200 XP, em cerca de 440 aventuras?!
Sejamos sinceros, alguém já jogou uma campanha de QUALQUER JOGO com mais de 100 aventuras? Não é impossível, mas é improvável: você teria que jogar uma vez por semana, todas as semanas durante dois anos, sem falta! Ninguém chega no nível 15. A não ser que você jogue de forma ininterrupta por 8 anos e meio uma vez por semana. O problema fica ainda maior para quem joga uma vez por mês: 36 anos e meio pra chegar no nível 15...
Bom, tem gosto pra tudo, até pra quem procura funções matemáticas num jogo de RPG. Jogadores não pensam em funções e algoritmos quando jogam RPG, mas quem projeta um jogo pensa, ou ao menos deveria. Parece que a Daemon não refletiu muito...
Com isso fica óbvia a disparidade na progressão do ganho de XP em relação à progressão de nível.
Soluções
Progressão Aritmética
A solução para o problema é fazer com que tanto a XP necessária para progredir de nível quanto o ritmo de ganho de XP adotem o mesmo tipo de progressão: ou o ganho de XP passa a ser polinomial, ou a progressão tem que ser aritmética. O problema da XP distribuída pelo Mestre ser polinomial é que Daemon não é matar-pilhar-destruir como D&D! Não dá pra inventar XP diferente pra cada coisa que ocorre numa aventura Daemon. Logo, a solução é mudar completamente a coluna de XP na Tabela de Avanço de Nível e torná-la aritmética, de modo que os personagens possam evoluir a cada 3 ou 4 aventuras, como sugeria o sistema nas primeiras edições, mas considerando ganhos médios de 5 XP por aventura.
Ao multiplicar o número de aventuras para o próximo nível pelo ganho médio de XP por aventura chegou-se nos números 15 e 20, respectivamente (3×5 e 4×5). Mantendo a XP dos níveis 1 e 2, fui somando 15 e 20, alternadamente, do nível 3 em diante, e depois mandei a planilha encontrar a equação. Chegou-se à função expressa no gráfico a seguir, onde "n" é o nível do personagem e "f(n)" a XP necessária para alcançar aquele nível. Os valores obtidos devem ser arredondados para o múltiplo inteiro de 5 mais próximo.
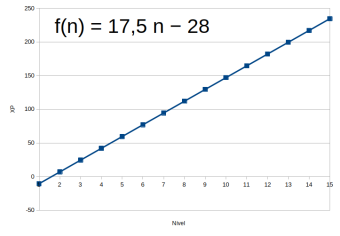
Na tabela obtida, com ganhos médios de XP, são necessárias 4 aventuras para passar do 2º ao 3º nível, 3 aventuras do 3º ao 4º, 4 aventuras do 4º ao 5º, e assim por diante (alternando 3 e 4 aventuras). Para chegar ao 10º nível, partindo do 1º, são necessárias, em média, 29 aventuras; 47 para o nível 15. Pode ser mais rápido se o Mestre for generoso com a XP. Bastante razoável.
A Tabela de Avanço de Nível baseada nessa equação segue abaixo:
| Nível | Pontos de Experiência (XP) | Aventuras necessárias p/ alcançar o próximo nível | Aventuras totais p/ alcançar o nível atual |
|---|---|---|---|
| 1 | 0 | 1 | 0 |
| 2 | 5 | 4 | 1 |
| 3 | 25 | 3 | 5 |
| 4 | 40 | 4 | 8 |
| 5 | 60 | 3 | 12 |
| 6 | 75 | 4 | 15 |
| 7 | 95 | 3 | 19 |
| 8 | 110 | 4 | 22 |
| 9 | 130 | 3 | 26 |
| 10 | 145 | 4 | 29 |
| 11 | 165 | 3 | 33 |
| 12 | 180 | 4 | 36 |
| 13 | 200 | 3 | 40 |
| 14 | 215 | 4 | 43 |
| 15 | 235 | 3 | 47 |
Aritmética simplificada
É possível simplificar ainda mais, adotando uma progressão linear de soma simples (+15 ou +20), em vez da soma alternada (+15/+20). Se, para passar de nível, forem necessários 15 XP/nível fixos, a função seria f(n) = 15(n-1). O resultado ainda seria bastante razoável: a passagem de nível se daria a cada 3 aventuras, considerando ganhos médios de 5 XP / aventura, e para chegar ao nível 15 seriam precisos 210 XP, que é quase o mesmo tanto do nível 14 (215 XP) na soma alternada acima.
Retorno às Raízes
Uma segunda solução, que representa um retorno às raízes do Sistema Daemon, seria abolir a XP. Assim como na 1ª e 2ª edições, é o mestre quem decidirá quando os PCs passam de nível, fazendo a avaliação de quando estão aptos.
Ele pode fazer isso da forma que melhor lhe convir. É possível determinar checkpoints (pontos de inspeção) e achievments' (conquistas) ocultos na campanha: locais, situações ou metas que o grupo atinge que permitem mover a narrativa de um ponto a outro, de uma aventura a outra. Adicionalmente ele também pode definir achievments individuais para cada personagem do jogador. Esse método é mais subjetivo, mas se adéqua bem ao sistema.
Referências
Publicado originalmente em:
- Daniel Dias Rodrigues ("Nerun") (11/07/2017, atual. 02/02/2024). GURPZine: Daemon: o problema da progressão em nível.